Proposição

Primeiramente, podemos conceituar proposição como sendo: “Toda oração declarativa que pode ser classificada em verdadeira ou em falsa.”

Sendo que toda proposição apresenta obrigatoriamente algumas características. São elas:

1. Por ser oração tem sujeito e predicado
2. É sempre declarativa. (não pode ser interrogativa e nem exclamativa)
3. Apresenta um único valor lógico: ou é verdadeira (V) ou falsa (F)

Observe alguns exemplos de preposições:

a) quinze é diferente de oito. () (V)

b) dois é divisor de nove. (2 | 9) (F)

c) cinco é maior do que três. (5 > 3) (V)

d) três é um número inteiro. () (V)

Exemplo de frases que não podem ser consideradas proposições:

e) duas vezes quatro mais 2. ()

f) duas vezes cinco igual a dez? (?)

g) o dobro de um número mais dois igual a seis. ()

o exemplo do item (e) não tem predicado, o item (f) é uma frase interrogativa e o item (g) não possui valor lógico.

Negação

Sempre será possível construir uma outra proposição a partir de uma proposição p qualquer. Esse outra proposição é denominada de negação de p e representada por ~p.

Exemplos:
a) p: Nove é diferente de cinco. (9 5) (V)
~p: Nove é igual a cinco. (9 = 5) (F)

b) p: Sete é maior que três. (7 > 3) (V)
~p: Sete é menor ou igual a três. (7 < 3) (F)

c) p: Dois é um número inteiro. () (V)
~p: Dois não é um número inteiro. () (F)

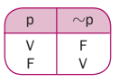
Observação: A proposição ~p tem sempre o valor oposto de p. Assim, ~p é verdadeira quando p é falsa e ~p é falsa quando p é verdadeira. Conforme mostra a “tabela-verdade” abaixo:

Certamente, você gostará de ler isso.